How Do You Know if Function Is One to One

One to One Function

The term i to one relationships actually refers to relationships between any ii items in which one can merely belong with only one other particular. In a mathematical sense, these relationships can exist referred to every bit 1 to one functions, in which there are equal numbers of items, or i item can only be paired with only one other item. The name of a person and the reserved seat number of that person in a train is a uncomplicated daily life example of one to 1 function.

If you lot are curious nigh what makes 1 to one functions special, then this article will help you learn almost their backdrop and appreciate these functions. Using solved examples, let united states of america explore how to identify these functions based on expressions and graphs.

ane.	What is a One to One Office?
2.	Horizontal Line Examination
3.	Backdrop of 1 to One Function
4.	How to Determine if a Function is I to One?
5.	One to Ane Function Graph
half-dozen.	Inverse of Ane to One Role
vii.	Steps to Find the Changed of One to Function
eight.	FAQs on Ane to I Function

What is a 1 to Ane Function?

A normal function can really have two different input values that can produce the same answer, whereas a one to 1 role does not. Let's go ahead and get-go with the definition and properties of ane to one functions.

1 to I Function Definition

I to one office is a special part that maps every chemical element of the range to exactly ane element of its domain i.e, the outputs never echo. As an example, the part g(ten) = ten - 4 is a one to 1 office since it produces a different respond for every input. Also, the function thousand(ten) = x² is non a 1 to one office since it produces 4 every bit the answer when the inputs are two and -ii. A office that is not one-to-i is called a many-to-ane function.

Algebraically, we can define one to ane office as:

office k: D -> F is said to be one-to-one if

• 1000(x_ane) = k(10_two) ⇒ ten_i = x_ii

for all elements x_i and x₂ ∈ D. A one to 1 role is too considered every bit an injection, i.eastward., a office is injective only if it is one-to-one. The contrapositive of this definition is a office m: D -> F is one-to-i if x₁ ≠ x₂ ⇒ g(10₁) ≠ thou(x₂). Permit us visualize this by mapping 2 pairs of values to compare functions that are and that are not one to one

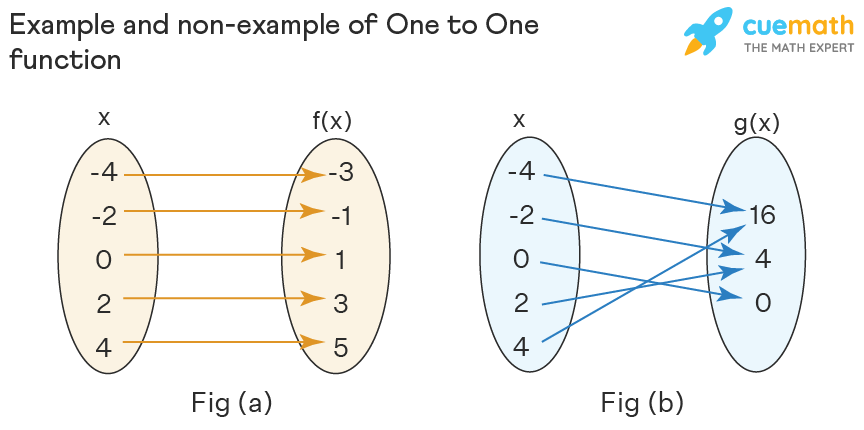
In the Fig (a), ten is the domain and f(ten) is the codomain, as well in Fig (b), ten is a domain and g(x) is a codomain.

In Fig(a), for each x value, there is only one unique value of f(x) and thus, f(x) is i to one function.

In Fig (b), different values of ten, two, and -2 are mapped with a mutual thousand(x) value 4 and (also, the dissimilar 10 values -iv and four are mapped to a mutual value 16). Thus, thou(x) is a function that is not a one to one function.

Horizontal Line Test

The horizontal line test is used to determine whether a function is one-one when its graph is given. Nosotros have already seen the condition (g(x₁) = k(x_ii) ⇒ 10_i = x₂) to make up one's mind whether a function thou(10) is one-one algebraically. On the other hand, to test whether the office is i-one from its graph,

• but take a horizontal line (consider a horizontal stick) and make information technology pass through the graph.
• If the horizontal line is NOT passing through more than ane point of the graph at any point in time, then the part is one-one.
• If the horizontal line passes through more than than one point of the graph at some point, so the function is Non one-ane.

In the in a higher place graph,

• f(10) = x² is Non 1-one equally it failed the horizontal line test (as the horizontal line passes through more than than one point of the graph)
• f(ten) = ten^three is i-one every bit information technology passed the horizontal line test (as the horizontal line passes through merely 1 point of the graph every fourth dimension)

Backdrop of One to 1 Part

A i-to-ane part i.e an injective function that maps the singled-out elements of its domain to the distinct elements of its co-domain. Here are some properties that aid u.s.a. to understand the various characteristics of one to one functions:

• If two functions, f(10) and k(x), are ane to 1, the composite function f ◦ g is a one to i function as well. (f ◦ yard) (x₁) = (f ◦ grand) (x₂) ⇒ f(k(ten_ane)) = f(k(ten₂)) ⇒ one thousand(x₁) = g(x₂) ⇒ x₁ = 10₂
• The domain of the part yard equals the range of g^-1 and the range of g equals the domain of g^-1
• If a function is considered to be one to ane, and then its graph will either be always increasing or always decreasing.
• g^-1 (g(x)) = ten, for every x in the domain of one thousand, and g(g^-1(x)) = x for every 10 in the domain of g^-ane.
• If f ◦ k is a ane to 1 part, then chiliad(10) is also guaranteed to exist a one to 1 function
• The graph of a office and the graph of its changed are symmetric with each other with respect to the line y = x.

How to Determine if a Function Is 1 to One?

Vertical line test are used to decide if a given relation is a part or not. Further, nosotros can determine if a part is one to 1 by using ii methods:

• Testing one to one function graphically: If the graph of k(x) passes through a unique value of y every time, then the function is said to be ane to ane part (horizontal line test).
• Testing i to one function algebraically: The function g is said to be one to 1 if a = b for every g(a) = 1000(b)

One to One Function Graph

Any function can exist represented in the form of a graph. This function is represented by drawing a line/a curve on a plane equally per the cartesian sytem. The domain is marked horizontally with reference to the x-axis and the range is marked vertically in the direction of the y-axis. If a function thousand is 1 to one role then no two points (ten₁, y_ane) and (10_ii, y₂) have the same y-value. Therefore no horizontal line cuts the graph of the equation y = k(x) more than one time. The following figure (the graph of the direct line y = x + 1) shows a 1-one office. Note that no ii points on it take the same y-coordinate (or) it passes the horizontal line test.

Changed of One to One Function

It is essential for one to understand the concept of one-to-one functions in order to understand the concept of inverse functions and to solve sure types of equations. Firstly, a role g has an changed function, m^-1, if and but if thousand is one to 1. In the below-given image, the inverse of a ane-to-i role g is denoted by g^−ane, where the ordered pairs of g^-1 are obtained past interchanging the coordinates in each ordered pair of yard. Here the domain of thou becomes the range of -i, and the range of g becomes the domain of 1000^-one.

Properties of the Changed of One to One Function

The inverse of ane to one function undoes what the original function did to a value in its domain in order to become back to the original y-value. Here are the properties of the inverse of one to i function:

• The function f has an inverse office if and only if f is a one to i function i.e, only one to one functions tin accept inverses.
• If the functions g and f are inverses of each other and so, both these functions can be considered equally one to one functions.
• If f and g are inverses of each other if and only if (f ◦ g) (x) = 10, x in the domain of one thousand and (chiliad ◦ f) (x) = x, x in the domain of f. Here f ◦ g is the composition function that has 'f' composed with '1000'. '
• If f and g are inverses of each other and then the domain of f is equal to the range of g and the range of one thousand is equal to the domain of f.
• If f and g are inverses of each other and so their graphs are volition brand reflections of each other on the line y = x.
• If the betoken (c, d) is on the graph of f and so bespeak (d, c) is on the graph of f^-1.

Steps to Find the Changed of One to I Function

The footstep by step procedure to derive the changed office k^-1(ten) for a one to ane role grand(x) is as follows:

• Set 1000(ten) equal to y
• Switch the x with y since every (x, y) has a (y, ten) partner
• Solve for y
• In the equation but found, rename y as g^-1 (10).

Example: Find the inverse part m^-i(ten) of the office g(10) = 2 ten + 5.

At present, let u.s.a. follow the iv steps:

Set g(x) equal to y	y = 2x + 5
Switch ten with y	x = 2y + five
Solve for y	y = (x - v)/2
Rename y as g-ane(x). This is the inverse.	g-1(x) = (y - 5)/2

Of import Notes on One to One Role:

Here is a listing of a few points that should be remembered while studying ane to one function:

• In a mathematical sense, one to i functions are functions in which in that location are equal numbers of items in the domain and in the range, or one can only be paired with another item.
• Information technology is essential for one to understand the concept of one to one functions in social club to empathise the concept of inverse functions and to solve certain types of equations.
• One can easily decide if a role is one to one geometrically and algebraically likewise.☛ Related Topics:

Check out the post-obit pages related to one to i office

• Graphing Functions
• Linear Functions
• Inverse Office Estimator

Examples on One to I Function

1. Example 1: Let D = {iii, four, 8, x} and C = {w, x, y, z}. Which of the post-obit relations represent a one to 1 function?

   {(3, westward), (3, x), (3, y), (3,z)}
   {(4,w), (iii,x), (10,z), (8, y)}
   {(4,w), (3,x), (8,ten), (10, y)}

   Solution:

   For a part to be a i to one office, each element from D must pair up with a unique element from C.

   • In the first relation, the same value of x is mapped with each value of y, so it cannot be considered as a role and, hence it is not a one-to-i function.
   • In the third relation, iii and 8 share the same range of 10. Hence, information technology is non a i-to-ane part.
   • The second relation maps a unique element from D for every unique element from C, thus representing a one-to-one part.

   Respond: Thus, {(iv,w), (3,x), (x,z), (8, y)} correspond a one to one office.

2. Instance 2: Make up one's mind if k(x) = -3x³ – i is a i to one part using the algebraic approach.

   Solution:

   In order for role to be a one to one function, g( x_one ) = g( x₂ ) if and simply if x_one = x_two . Allow us showtime solving now:

   g( x_ane ) = -3 x_i ³ – 1

   grand( x₂ ) = -3 10_two ³ – ane

   We volition first with m( x₁ ) = thousand( x₂ ). Then

   -iii x₁ ³ – one = -3 x₂ ³ – 1

   -3 x_one ³ = -3 ten₂ ³

   ( x₁ )³ = ( x₂ )³

   Removing the cube roots from both sides of the equation volition lead us to x_one = ten₂.

   Reply: Hence, grand(ten) = -3x³ – 1 is a 1 to one office.

3. Example 3: If the role in Example 2 is one to i, detect its changed. Likewise, determine whether the inverse part is one to one.

   Solution:

   Allow g(10) = y. Then y = -3xⁱⁱⁱ – 1.

   Interchange x and y:

   x = -3y^three – 1

   10 + 1 = -3y³

   (-x - i) / 3 = y³

   y = ∛[(-x - 1) / 3] = 1000^-1(ten)

   To determine whether information technology is ane to one, let the states assume that g^-1( x₁ ) = one thousand^-1( ten_two ).

   ∛[(-x₁ - 1) / 3] = ∛[(-x₂ - 1) / 3]

   Cubing on both sides,

   (-x₁ - 1) / 3 = (-x₂ - 1) / iii

   Multiplying by iii on both sides,

   -ten_ane - i = -x₂ - 1

   Adding 1 on both sides,

   -10₁ = -x_ii

   Multiplying both sides past -1,

   x₁ = x₂

   Hence g^-1(x) is one to 1.

   Answer: Inverse of grand(ten) is found and it is proved to exist 1-1.

go to slidego to slidego to slide

Corking learning in high school using simple cues

Indulging in rote learning, you are likely to forget concepts. With Cuemath, yous volition learn visually and be surprised by the outcomes.

Book a Free Trial Class

Practice Questions on Ane to Ane Function

go to slidego to slide

FAQs on One to One Function

What Is the Definition of I to One Function?

One to 1 functions are special functions that maps every element of range to a unit element of the domain. It means, a function y = f(10) is one-one just when for no 2 values of ten and y, nosotros take f(x) equal to f(y). A normal office can actually have two different input values that tin produce the aforementioned answer, whereas a one to 1 function does not.

What is the Departure Between Vertical Line Test and the Horizontal Line Examination?

Hither are the differences betwixt the vertical line test and the horizontal line test.

Vertical Line Test	Horizontal Line Test
The vertical line test is used to determine whether a relation is a function.	The horizontal line test is used to determine whether a function is one-1.
To use this examination, make a vertical line to pass through the graph and if the vertical line does NOT meet the graph at more than one signal at any instance, then the graph is a role.	To apply this test, make a horizontal line to pass through the graph and if the horizontal line does NOT see the graph at more than one point at whatsoever instance, and so the graph is a 1 to ane function.

How Do You Bank check if a Function Is One to One?

One can check if a function is ane to 1 by using either of these two methods:

• Testing one to one part geometrically: If the graph of the role passes the horizontal line examination then the function tin be considered as a one to one function.
• Testing ane to one role algebraically: The function yard is said to be one to one if for every g(x) = chiliad(y), x = y.

What Types of Functions Are 1 to One Functions?

A i to one office is either strictly decreasing or strictly increasing.

• If f(x) is increasing, then f '(x) > 0, for every ten in its domain
• If f(ten) is decreasing, then f '(x) < 0, for every x in its domain

In a one to 1 office, the aforementioned values are non assigned to two different domain elements.

What Does It Mean if a Office Is Not One to One Office?

In a office, if a horizontal line passes through the graph of the function more than once, so the role is non considered equally 1-to-one function. A function that is non a 1 to one is considered every bit many to 1.

What Are the Steps in Solving the Changed of a One to I Function?

These are the steps in solving the inverse of a 1 to i function g(x):

• Ready thou(10) equal to y
• Interchange x and y.
• Solve the equation for y. If there is only one solution and so the inverse can exist; otherwise, it tin't.
• In the equation but institute, rename y as g^-ane (x).

What Is an Example of a Ane to One Function?

The function f(x) = x + five is a one to i part as information technology produces dissimilar output for a different input x. And for a part to exist 1 to one information technology must return a unique range for each chemical element in its domain. Here, f(x) returns half-dozen if x is one, seven if x is ii and so on. A person and his shadow is a real-life example of one to ane function.

What Is Not a 1 to One Function?

The function f(ten) = x² is non a one to one function equally it produces 9 as the respond when the inputs are 3 and -3. And for a role to be one to one it must return a unique range for each chemical element in its domain. Here, f(x) returns nine as an answer, for two dissimilar input values of three and -three.

Are Parabolas Ane to One Functions?

No, parabolas are non one to ane functions. The function g(y) = y^two is non i-to-ane function because k(2) = 1000(-ii). The role m(y) = y² graph is a parabolic function, and a horizontal line laissez passer through the parabola twice.

How Can We Apply the Concept of One to One Function in Daily Life?

We can meet these one to one relationships everywhere. I of the very common examples of a one to 1 human relationship that we come across in our everyday lives is where i person has 1 passport for themselves, and that passport is only to be used by this ane person.

oliverhealf1938.blogspot.com

Source: https://www.cuemath.com/algebra/one-to-one-function/

Share this post